Java基础

数据结构

数组
栈
队列
链表
树
图
字典树
散列表（哈希表）

排序算法

冒泡排序

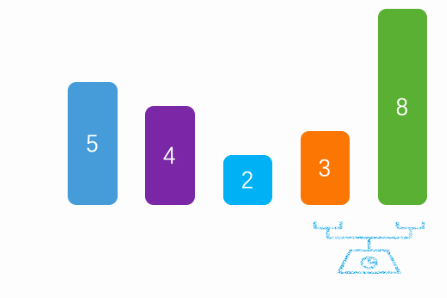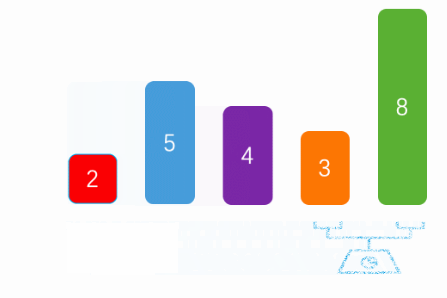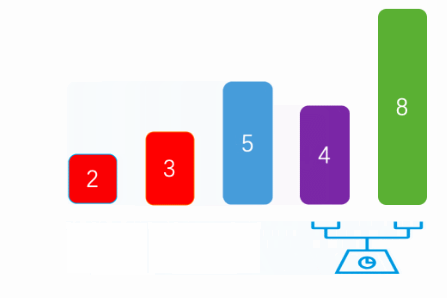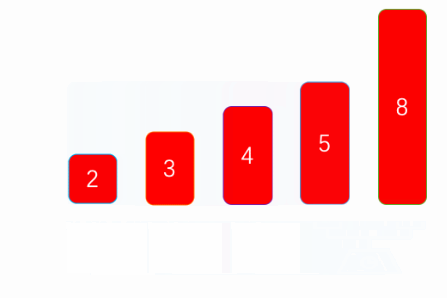
1、冒泡排序，是通过每一次遍历获取最大/最小值
2、将最大值/最小值放在尾部/头部
3、然后除开最大值/最小值，剩下的数据在进行遍历获取最大/最小值

代码

public static void main(String[] args) {

        int arr[] = {8, 5, 3, 2, 4};

        //冒泡
        for (int i = 0; i < arr.length; i++) {
            //外层循环，遍历次数
            for (int j = 0; j < arr.length - i - 1; j++) {
                //内层循环，升序（如果前一个值比后一个值大，则交换）
                //内层循环一次，获取一个最大值
                if (arr[j] > arr[j + 1]) {
                    int temp = arr[j + 1];
                    arr[j + 1] = arr[j];
                    arr[j] = temp;
                }
            }
        }
    }

选择排序

将第一个值看成最小值
然后和后续的比较找出最小值和下标
交换本次遍历的起始值和最小值
说明：每次遍历的时候，将前面找出的最小值，看成一个有序的列表，后面的看成无序的列表，然后每次遍历无序列表找出最小值。

代码

public static void main(String[] args) {

        int arr[] = {6, 5, 3, 2, 4};

        //选择
        for (int i = 0; i < arr.length; i++) {
            //默认第一个是最小的。
            int min = arr[i];
            //记录最小的下标
            int index = i;
            //通过与后面的数据进行比较得出，最小值和下标
            for (int j = i + 1; j < arr.length; j++) {
                if (min > arr[j]) {
                    min = arr[j];
                    index = j;
                }
            }
            //然后将最小值与本次循环的，开始值交换
            int temp = arr[i];
            arr[i] = min;
            arr[index] = temp;
            //说明：将i前面的数据看成一个排好的队列，i后面的看成一个无序队列。每次只需要找无需的最小值，做替换
        }
    }

插入排序

默认从第二个数据开始比较。
如果第二个数据比第一个小，则交换。然后在用第三个数据比较，如果比前面小，则插入（狡猾）。否则，退出循环
说明：默认将第一数据看成有序列表，后面无序的列表循环每一个数据，如果比前面的数据小则插入（交换）。否则退出。

代码

public static void main(String[] args) {

        int arr[] = {7, 5, 3, 2, 4};

        //插入排序
        for (int i = 1; i < arr.length; i++) {
            //外层循环，从第二个开始比较
            for (int j = i; j > 0; j--) {
                //内存循环，与前面排好序的数据比较，如果后面的数据小于前面的则交换
                if (arr[j] < arr[j - 1]) {
                    int temp = arr[j - 1];
                    arr[j - 1] = arr[j];
                    arr[j] = temp;
                } else {
                    //如果不小于，说明插入完毕，退出内层循环
                    break;
                }
            }
        }
    }

希尔排序

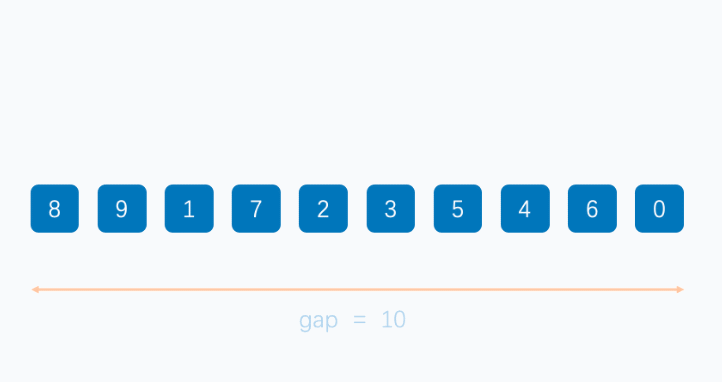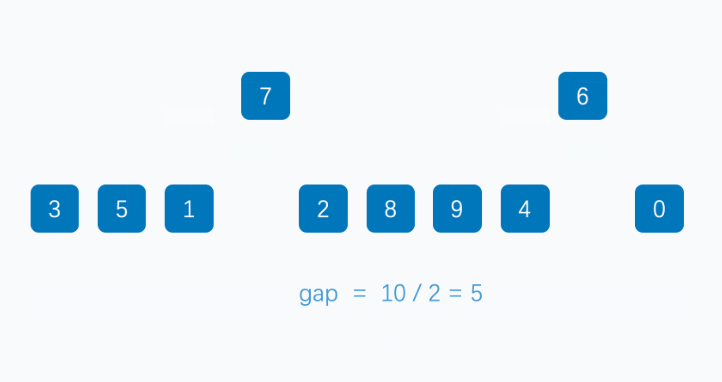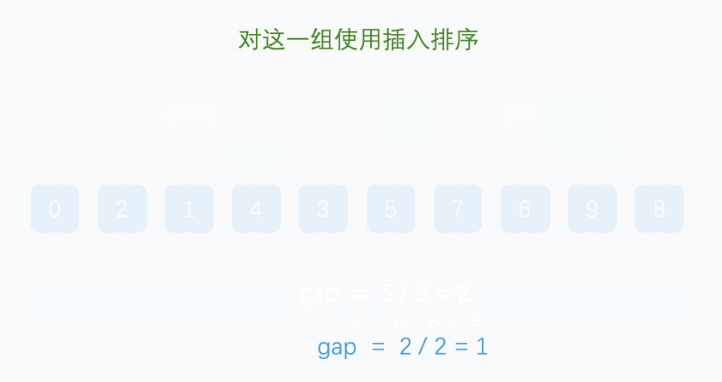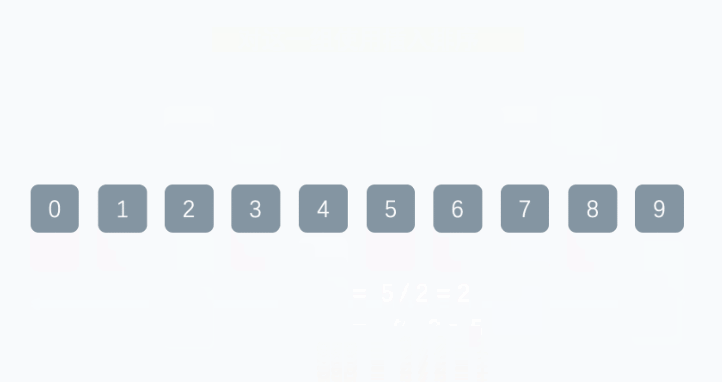
基本上和插入排序一样的道理
不一样的地方在于，每次循环的步长，通过减半的方式来实现
说明：基本原理和插入排序类似，不一样的地方在于。通过间隔多个数据来进行插入排序。

代码

public static void main(String[] args) {

        int arr[] = {7, 5, 3, 2, 4};

        //希尔排序（插入排序变种版）
        for (int i = arr.length / 2; i > 0; i /= 2) {
            //i层循环控制步长
            for (int j = i; j < arr.length; j++) {
                //j控制无序端的起始位置
                for (int k = j; k > 0  && k - i >= 0; k -= i) {
                    if (arr[k] < arr[k - i]) {
                        int temp = arr[k - i];
                        arr[k - i] = arr[k];
                        arr[k] = temp;
                    } else {
                        break;
                    }
                }
            }
            //j,k为插入排序，不过步长为i
        }
    }

快速排序

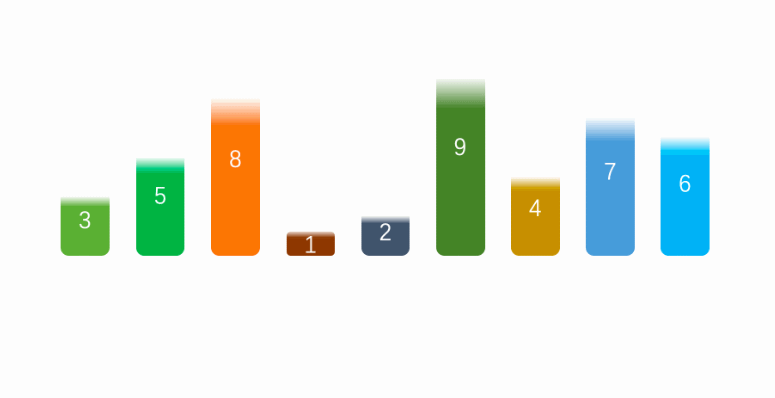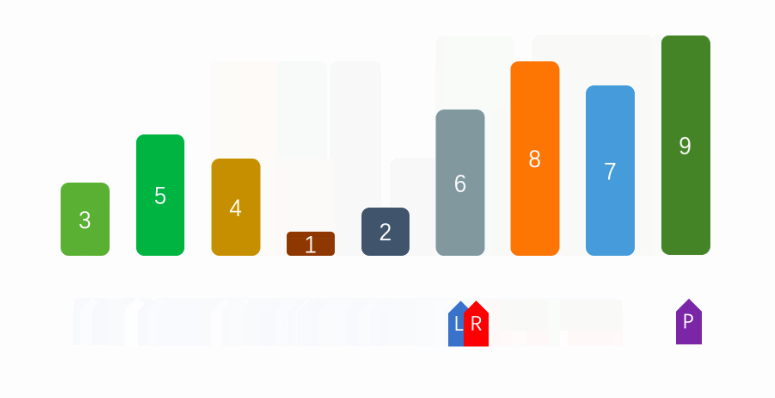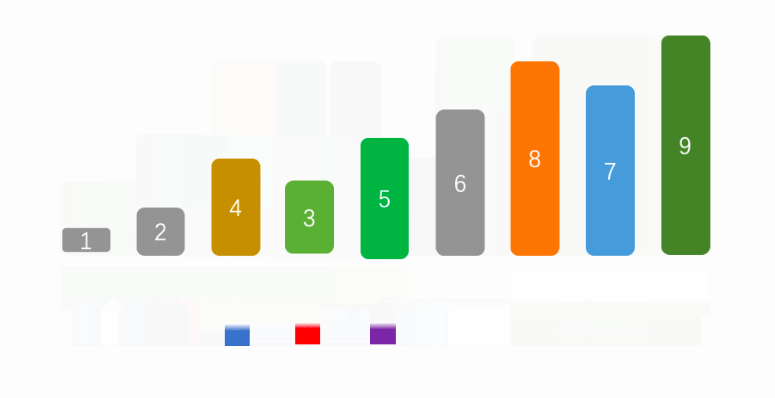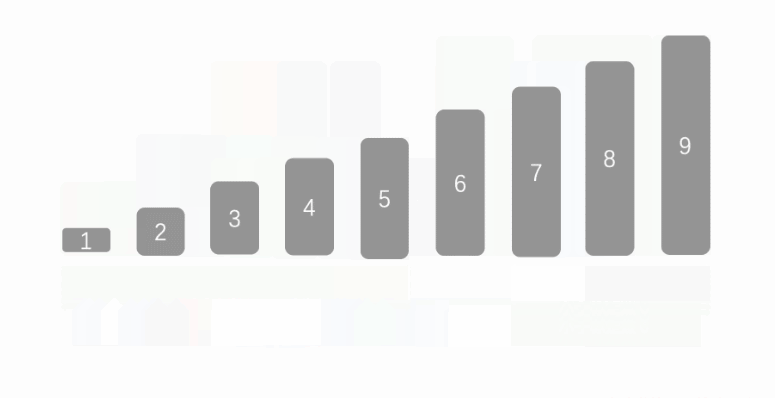
确认列表第一个数据为中间值，第一个值看成空缺（低指针空缺）。
然后在剩下的队列中，看成有左右两个指针（高低）。
开始高指针向左移动，如果遇到小于中间值的数据，则将这个数据赋值到低指针空缺，并且将高指针的数据看成空缺值（高指针空缺）。然后先向右移动一下低指针，并且切换低指针移动。
当低指针移动到大于中间值的时候，赋值到高指针空缺的地方。然后先高指针向左移动，并且切换高指针移动。重复c、d操作。
直到高指针和低指针相等时退出，并且将中间值赋值给对应指针位置。
然后将中间值的左右两边看成行的列表，进行快速排序操作。

代码

public static void main(String[] args) {

        int arr[] = {7, 5, 3, 2, 4, 1, 8, 9, 6};

        //快速排序
        int low = 0;
        int high = arr.length - 1;
        quickSort(arr, low, high);  
    }

    public static void quickSort(int[] arr, int low, int high) {
        //如果指针在同一位置(只有一个数据时)，退出
        if (high - low < 1) {
            return;
        }
        //标记，从高指针开始，还是低指针（默认高指针）
        boolean flag = true;
        //记录指针的其实位置
        int start = low;
        int end = high;
        //默认中间值为低指针的第一个值
        int midValue = arr[low];
        while (true) {
            //高指针移动
            if (flag) {
                //如果列表右方的数据大于中间值，则向左移动
                if (arr[high] > midValue) {
                    high--;
                } else if (arr[high] < midValue) {
                    //如果小于，则覆盖最开始的低指针值，并且移动低指针，标志位改成从低指针开始移动
                    arr[low] = arr[high];
                    low++;
                    flag = false;
                }
            } else {
                //如果低指针数据小于中间值，则低指针向右移动
                if (arr[low] < midValue) {
                    low++;
                } else if (arr[low] > midValue) {
                    //如果低指针的值大于中间值，则覆盖高指针停留时的数据，并向左移动高指针。切换为高指针移动
                    arr[high] = arr[low];
                    high--;
                    flag = true;
                }
            }
            //当两个指针的位置相同时，则找到了中间值的位置，并退出循环
            if (low == high) {
                arr[low] = midValue;
                break;
            }
        }
        //然后出现有，中间值左边的小于中间值。右边的大于中间值。
        //然后在对左右两边的列表在进行快速排序
        quickSort(arr, start, low -1);
        quickSort(arr, low + 1, end);
    }

归并排序

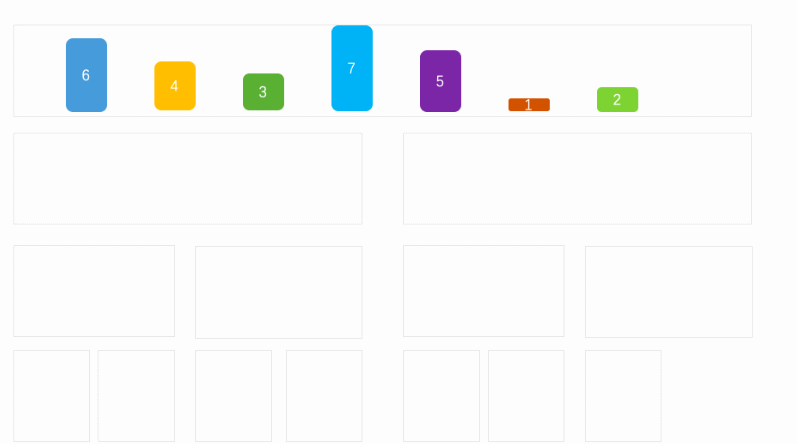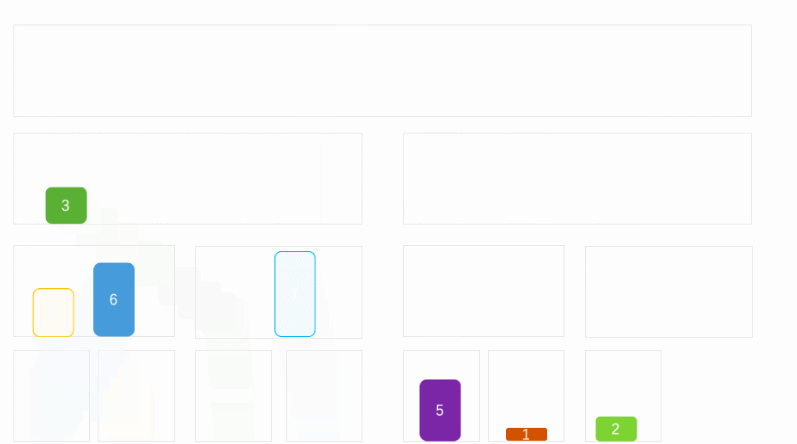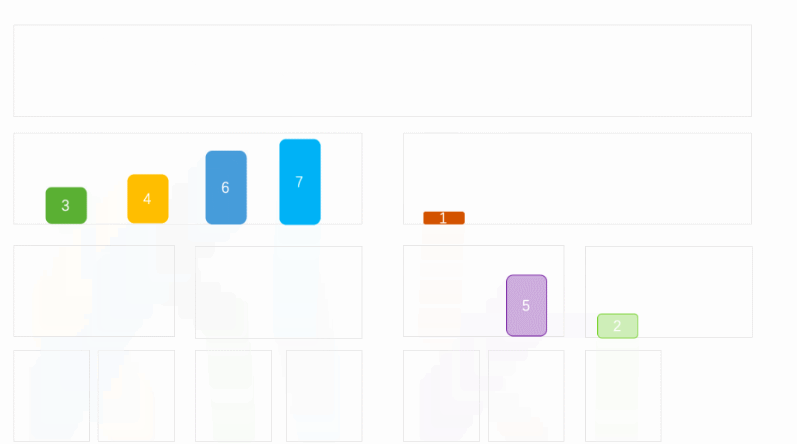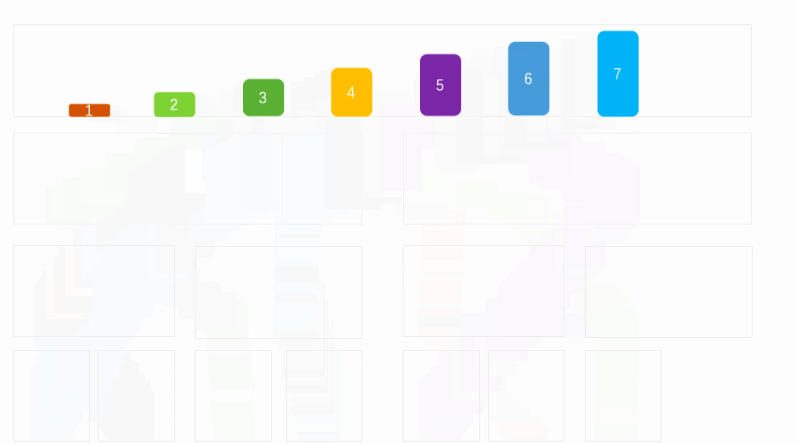
将列表按照对等的方式进行拆分
拆分小最小快的时候，在将最小块按照原来的拆分，进行合并
合并的时候，通过左右两块的左边开始比较大小。小的数据放入新的块中
说明：简单一点就是先对半拆成最小单位，然后将两半数据合并成一个有序的列表。

代码

public static void main(String[] args) {

        int arr[] = {7, 5, 3, 2, 4, 1，6};

        //归并排序
        int start = 0;
        int end = arr.length - 1;
        mergeSort(arr, start, end);
    }

    public static void mergeSort(int[] arr, int start, int end) {
        //判断拆分的不为最小单位
        if (end - start > 0) {
            //再一次拆分，知道拆成一个一个的数据
            mergeSort(arr, start, (start + end) / 2);
            mergeSort(arr, (start + end) / 2 + 1, end);
            //记录开始/结束位置
            int left = start;
            int right = (start + end) / 2 + 1;
            //记录每个小单位的排序结果
            int index = 0;
            int[] result = new int[end - start + 1];
            //如果查分后的两块数据，都还存在
            while (left <= (start + end) / 2 && right <= end) {
                //比较两块数据的大小，然后赋值，并且移动下标
                if (arr[left] <= arr[right]) {
                    result[index] = arr[left];
                    left++;
                } else {
                    result[index] = arr[right];
                    right++;
                }
                //移动单位记录的下标
                index++;
            }
            //当某一块数据不存在了时
            while (left <= (start + end) / 2 || right <= end) {
                //直接赋值到记录下标
                if (left <= (start + end) / 2) {
                    result[index] = arr[left];
                    left++;
                } else {
                    result[index] = arr[right];
                    right++;
                }
                index++;
            }
            //最后将新的数据赋值给原来的列表，并且是对应分块后的下标。
            for (int i = start; i <= end; i++) {
                arr[i] = result[i - start];
            }
        }
    }